Geh aufs Ganze ist zurück – das Ziegenproblem auch

Freitags ist bei uns in der Familie Fernsehabend. Unsere Kinder entschieden sich an diesem Freitag, die Spielshow Geh aufs Ganze, die nun nach 18 Jahren erstmals wieder ausgestrahlt wurde, zu schauen. Mein Mann und ich fühlten uns ca. 25 Jahre in unsere Jugend zurückversetzt, aber wir schauten mit.

Spannend wurde es am Ende. Drei Tore, hinter denen sich ein Trostpreis, ein Zonk und ein Auto als Hauptgewinn befanden, standen zur Auswahl. Die Kandidatin wählte Tor 2. Daraufhin öffnete Jörg Draeger das Tor 1, hinter dem sich der Trostpreis befand. Nun wurde die Kandidatin gefragt, ob sie sich umentscheiden und doch lieber Tor 3 nehmen wolle. Sie blieb bei Tor 2.

In der folgenden Werbepause wurde bei uns in der Familie heiß diskutiert. Ich sagte, dass sich die Kandidatin umentscheiden solle, da man mit der Strategie des Umentscheidens eine höhere Gewinnwahrscheinlichkeit habe. Vor allem mein Mann hielt dagegen, da die Kandidatin ja bei zwei geschlossenen Toren eine 50:50-Chance habe, das Auto zu gewinnen. Das spannende und in der Mathematik unter dem Namen „Ziegenproblem“ oder „Drei-Türen-Problem“ bekannte Problem war zurück. Es wurde in unserer Familie genauso kontrovers diskutiert wie bereits am Ende des 20. Jahrhunderts, als das Ziegenproblem erstmals aufkam. Mein Mathematikerinnenherz freute sich. Interessant ist, dass ich erst in der letzten Woche mit meinen Studierenden im Rahmen einer geplanten Unterrichtseinheit zu bedingten Wahrscheinlichkeiten über das Ziegenproblem gesprochen hatte, und sie der Meinung waren, dass doch eigentlich alle mittlerweile wüssten, dass sich das Umentscheiden lohne. Dem ist offensichtlich nicht so.

Nach der Werbung ging es weiter. Die Kandidatin bleib weiterhin bei Tor 2. Das Tor 3 wurde geöffnet und dahinter befand sich der Hauptgewinn. Die Kandidatin konnte also nur den Zonk mit nach Hause nehmen. „Ach, du hattest also doch recht“, hieß es nun bei uns in der Familie. Natürlich kann man diese Aussage aus dem Ausgang dieser einen Show nicht ableiten. Der Ausgang der Show führte jedoch dazu, dass meine Familie wissen wollte, warum meiner Meinung nach das Umentscheiden die bessere Strategie sei.

Ich holte also meine für den Unterricht gebastelten Tore raus und wir spielten das Spiel mehrmals nach.

So mache ich es auch im Unterricht. Ich lasse die Schüler*innen zu zweit dreißigmal das Spiel mit der Strategie „Nicht umentscheiden“ und dreißigmal mit der Strategie „Umentscheiden“ spielen. Der Einfachheit halber wähle ich zwei Zonks bzw. Ziegen. Den Trostpreis möchte ja sowieso niemand. Bereits nach einer so niedrigen Zahl an Versuchsdurchführungen lässt sich in der Regel erkennen, dass die relative Häufigkeit für den Gewinn bei der Strategie „Umentscheiden“ höher ist als bei der Strategie „nicht umentscheiden“. Wir interpretieren hier die relative Häufigkeit als Schätzwert für die Wahrscheinlichkeit.

Um zu verstehen, warum das Umentscheiden tatsächlich sinnvoll ist, müssen Schüler*innen aber in die Rolle des Moderators schlüpfen und das Spiel mehrmals aus seiner Sicht spielen. Wenn ein Kandidat die Strategie „Nicht umentscheiden“ wählt, dann hat er eine Gewinnwahrscheinlichkeit von , denn von den drei Toren, die er auswählen kann, befindet sich in einem das Auto. Daran ändert auch die Tatsache nichts, dass später ein Tor geöffnet wird, denn der Kandidat entscheidet sich ja sowieso nicht um. Man könnte sich also vorstellen, dass er von allem, was nach seiner Entscheidung passiert, nichts mitbekommt. Seine Gewinnwahrscheinlichkeit liegt bei .

Wenn nun der Kandidat die Strategie „Umentscheiden“ wählt, gibt es zwei Möglichkeiten:

1. Der Kandidat hat mit seiner ersten Entscheidung ein Tor gewählt, hinter dem sich das Auto befindet. Die Wahrscheinlichkeit dafür liegt bei . Der Moderator, der ja weiß, hinter welchem Tor sich der Hauptgewinn befindet, hat nun zwei Möglichkeiten: Er kann eines der beiden noch verschlossenen Tore öffnen, hinter denen sich der Zonk befindet. Es ist egal, welches er öffnet. Der Kandidat entscheidet sich anschließend um und zwar leider für das weitere Tor, hinter dem sich ein Zonk befindet. Zusammenfassend kann man also festhalten, dass der Kandidat bei der Strategie „Umentscheiden“ immer dann verliert, wenn er bei seiner ersten Entscheidung das richtige Tor gewählt hat.

2. Der Kandidat wählt bei seiner ersten Entscheidung ein Tor, hinter dem sich ein Zonk befindet. Die Wahrscheinlichkeit dafür beträgt . Nun muss der Moderator, der ja weiß, hinter welchen Toren sich der Zonk und das Auto befinden, ein weiteres Tor öffnen. Nun kommt das Entscheidende: Der Moderator kann nur ein einziges Tor öffnen, nämlich das Tor mit dem zweiten Zonk, denn er darf ja weder das vom Kandidaten gewählte Tor noch das mit dem Auto öffnen. Wenn der Kandidat sich nun umentscheidet, entscheidet er sich automatisch für das noch verschlossene Tor, hinter dem sich das Auto befindet. Der Kandidat gewinnt folglich immer dann, wenn er bei der ersten Entscheidung ein falsches Tor ausgewählt hat. Die Wahrscheinlichkeit dafür beträgt .

Im Unterricht veranschaulichen wir die Situation anschließend mit einem je nach Klassenstufe unterschiedlich vorstrukturierten Baumdiagramm. Am anschaulichsten ist es, mit absoluten Häufigkeiten, z.B. mit 90 Spielen, zu arbeiten. So könnte beispielsweise ein Baumdiagramm für die Strategie „Umentscheiden“ aussehen:

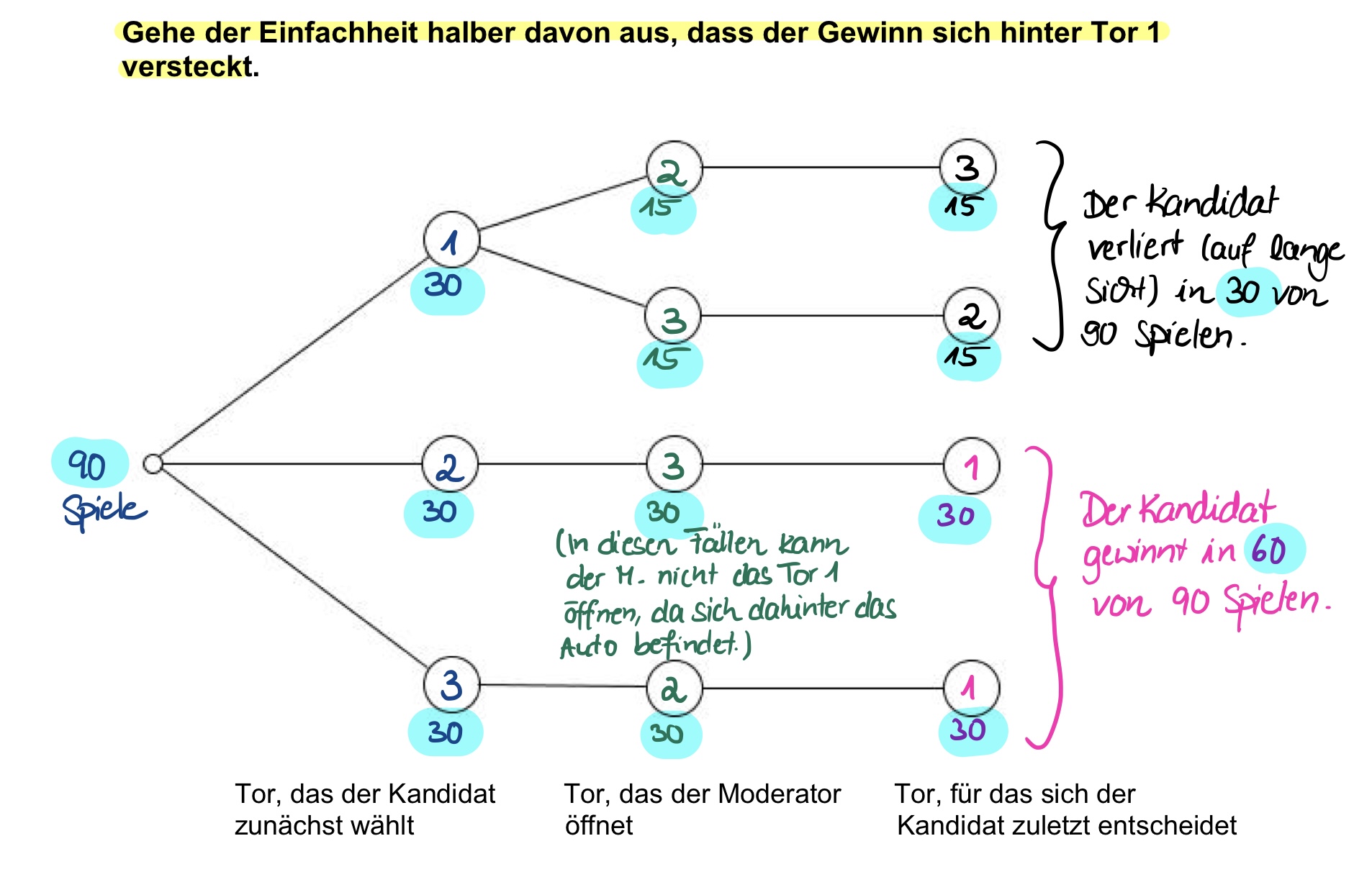
Oder das entsprechende Baumdiagramm mit Wahrscheinlichkeiten:

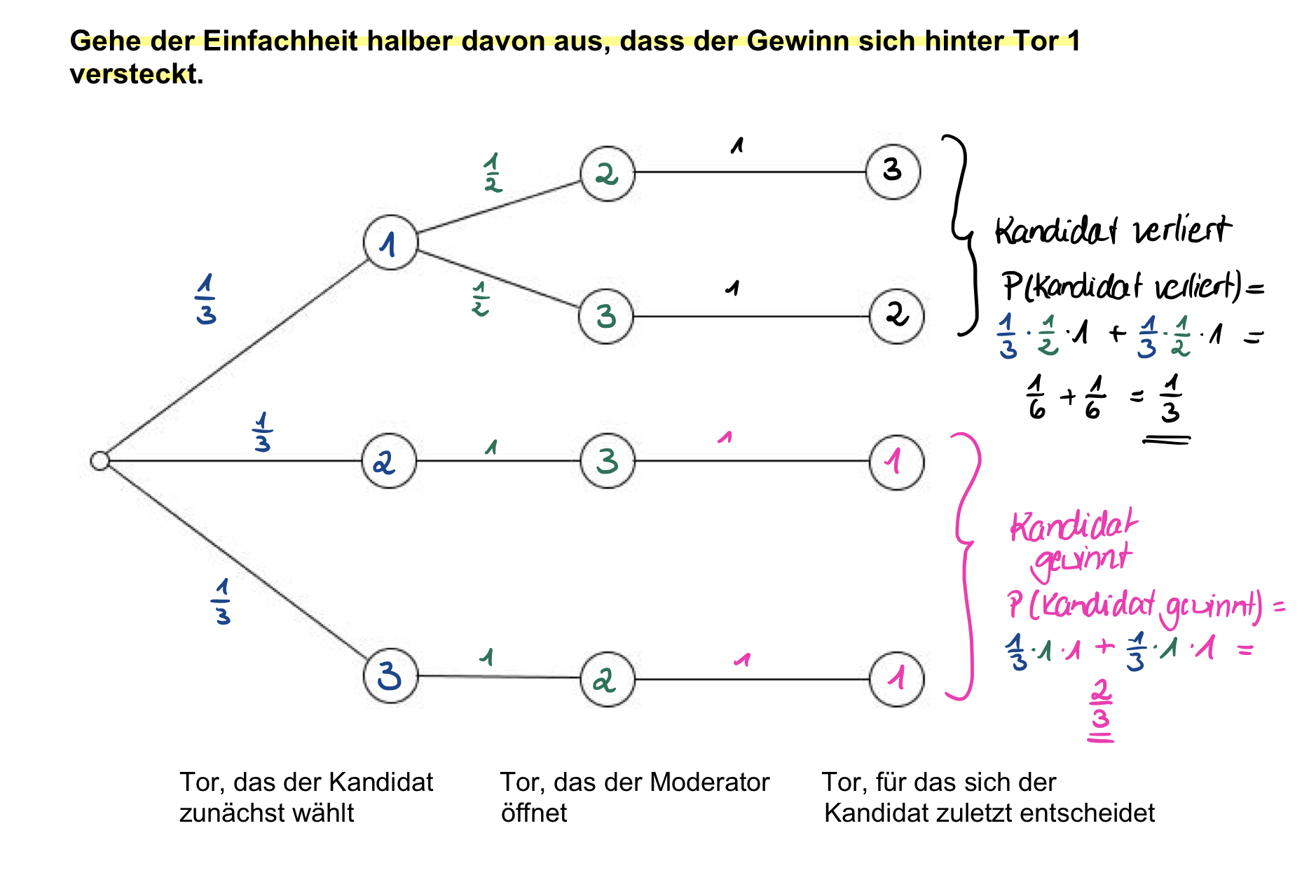
Natürlich gibt es eine Menge weiterer Erklärungsansätze, deren Betrachtung mathematisches Kommunizieren und Argumentieren fördert (wie z.B. die Idee, das Spiel auf 100 Tore zu übertragen, von denen 98 geöffnet werden). Auch diese lohnt es sich, zu besprechen. Für mich bleibt aber wichtig: Schüler*innen müssen das Spiel zunächst spielen, um die Unterschiede beider Strategien zu erfahren.

Ich freue mich schon darauf, das nächste Mal das Ziegenproblem zu unterrichten. Bestimmt wähle ich dann als Einstieg einen Ausschnitt der Sendung Geh aufs Ganze. Wenn mithilfe von Mathematik Situationen aus dem realen Leben erklärt werden können, dann ist Mathematikunterricht sinnstiftend.